A Chess Puzzle, Part IV: A Group of Rooks

Part IV of A Mathematical Chess Puzzle:

• Part I: The Infinite Chess Board
• Part II: Ruminations
• Part III: The Pawns, Knights and Kings
• Part IV: A Group of Rooks
• Part V: Rooks and Topology
• Part VI: The Bishop
• Part VII Episode 1: The Fractal Queen
• Part VII Episode 2: The Rational Super Queen
• Part VIII Conclusion: The Transfinite Super Queen and Beyond

Review

We have been studying the (classic) “unguarded” chess puzzle, which is to say, of packing as many of one chess piece on a chess board without any of the pieces attacking any others. What we have been doing is to measure the “density” $\delta$ of the pieces on the $n \times n$ chess board, as $n \rightarrow \infty$. So far we have shown that the densities for the Pawn, Knight and King are 1/2, 1/2, and 1/4 respectively, and also shown what such solutions look like on the infinite board.

In this post we will start to look at the other three pieces, Rooks, Bishops, and Queens, and will see how different things become. The reason things are different is that, unlike the Pawn, Knight and King, these remaining pieces have a “control region” which is unlimited, and extends out infinitely on an infinite board.

Our first clue that things are different may be seen by this analogous result from the previous post:

The Chess Density Theorem – Rooks, Bishops and Queens

DENSITY THEOREM 2: For Rooks, Bishops and Queens, their asymptotic density $\delta$ on the infinite board ($B_{\omega}$) is given by:

$\delta = 0$.

In other words, on an infinite chess board, the fraction of squares you can cover with “friendly” Rooks, Bishops or Queens is vanishingly small. As a reminder, by “friendly” I mean that none of the pieces are threatening each other by standard chess rules. Also, if you were to throw a dart at the board with a densest packing of friendly pieces, the odds of hitting a nonempty square is zero.

PROOF: Unlike the Pawns, Knights and Kings, the proof of this theorem is practically a one liner, as we can easily show that for each piece X in the set {R,B,Q}, there is a constant C>0 so that if $\Phi \in \mathscr{U}(B_n,X)$ is an unguarded chess position of that piece on the n-Board, then its weight (ie, the number of pieces in the position) $\Vert \Phi \Vert$  is bounded by

$$\Vert \Phi \Vert \le C*n$$

And so the density $\delta_n$ on the n-board is bounded by

$$ \delta_n = \frac{\Vert \Phi \Vert}{n^2} \le C/n$$

and so, since $C$ is a constant, then the quotient $C/n \rightarrow 0$ as $n \rightarrow \infty$.

For Rooks and Queens, the constant $C=1$ will do, because the n board has n rows, and neither rooks nor queens can share a row. For Bishops, the constant $C=2$ will do, because there are exactly $2n-1$ northwest diagonals on the n-board, and friendly bishops cannot share a diagonal. $\blacksquare$

Okay, so friendly Rooks, Bishops, and Queens have to be very sparse on the infinite board. But what do their solutions look like?

The Rook

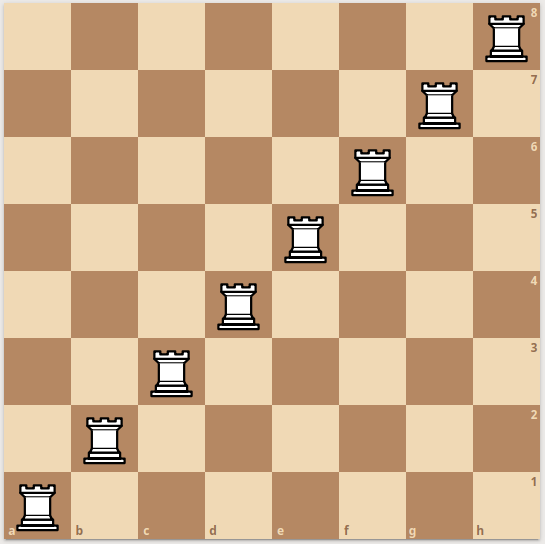
From part one we already know at least what one unguarded Rook solution looks like on the 8-board:

Which immediately suggests a general solution on the infinite board:

$$\Phi_R(x,y)=
\begin{cases}
R, & \text{if $x = y$} \\
\varnothing, & \text{otherwise}
\end{cases}\tag{Rook}
$$

On the infinite board the position looks like this (the diagonal line is infinitely thin):

We can readily see that this is indeed a solution, and it is also apparent that except for that infinitely thin line of rooks the board is empty. But are there any other solutions? There are, and they have a very interesting characteristic. At least for me…

Let’s start with a definition:

DEFINITION: A chess position $\Phi$ on a board B is said to have the Rook Property if and only if every row and column of B has exactly one non-empty square.

Obviously, any maximally unguarded Rook positions have the Rook property. But this is also a property of maximally unguarded Queens, so the definition is a bit more general.

If you think about it, if a position $\Phi$ has the Rook Property on the n-Board, then this means for any integer $x$ between 0 and $n-1$, there is exactly one integer $y$ in that same range so that $\Phi(x,y)$ is a non-empty piece. In other words, $y$ is a function of $x$, so that we can write $y = \phi(x)$. And not only that, but since no two non-empty squares of $\Phi$ can have the same row (y-value), this means that if $\phi(x_1)= \phi(x_2)$, then $x_1= x_2$. In other words, the function $\phi(x)$ is also an invertible function (bijection) from the set {0,1,….n-1} to itself.

Such functions $\phi(x)$ have a more common name, which is that they are permutations (rearrangements) of the set of n elements. The set of all permutations form what is called the symmetry group Sym(n), and it appears all over the place in group theory.

A group is simply a set $G$, together with a “group product” often denoted $a{\circ}b$, with the property that (1) there is an “identity” element $e$ for which $e{\circ}a = a{\circ}e = a$ for all $a \in G$, (2) for every $a \in G$ there is an “inverse” $a’$, so that $a’{\circ}a = a{\circ}a’ = e$, and (3) the product is associative, ie $(a{\circ}b)\circ c= a{\circ}(b \circ c)$. The integers and addition are an example. Group theory has a lot of uses.

In any case, it can (easily) be proved that this relationship between $\Phi(x,y)$ and $\phi(x)$works both ways, on any board:

THE ROOK GROUP THEOREM: If $A$ is any set (finite or infinite), $\Phi$ is a position on the board $B_A$, then $\Phi$ has the Rook Property if and only if there is a permutation $\phi \in Sym(A)$ such that the position $\Phi$ satisfies the following:

$$ \forall x,y \in A: \Phi(x,y) \neq \varnothing \text{ if and only if } y=\phi(x)$$

In particular, if consider only rook positions on a board $B_A$, then there is an exact one to one correspondence between the maximally unguarded positions and elements of the symmetry group $Sym(A)$. In other words, the set of maximal friendly Rook positions forms a group, and you can actually define a group operator (*) on solutions so that the group product of two such solutions forms another solution!

In fact, if you inspect the one example we showed for eight rooks on the standard 8-board, you can see that it corresponds to the identity element of Sym(8), ie, $\phi(x) = x$.

This may all sound like gobbledegook, but it gives us some simple ways to cook up new examples of friendly Rook positions. For the eight board, all we need to do is write down a couple of permutations of the set {0,1,…8}.

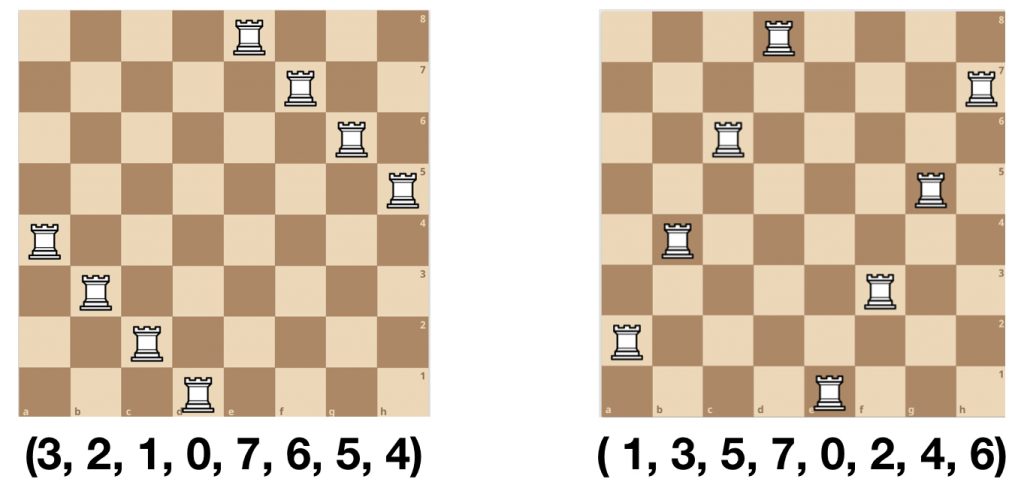
For example consider the following two permutations:

(3,2,1,0,7,6,5,4) and  (1,3,5,7,0,2,4,6).

These can be thought of as two functions, each being the ordered list of values you get by plugging in 0, then 1, then 2, and so on. The chess positions that correspond to them, are simply the graph of the functions on the board, like this:

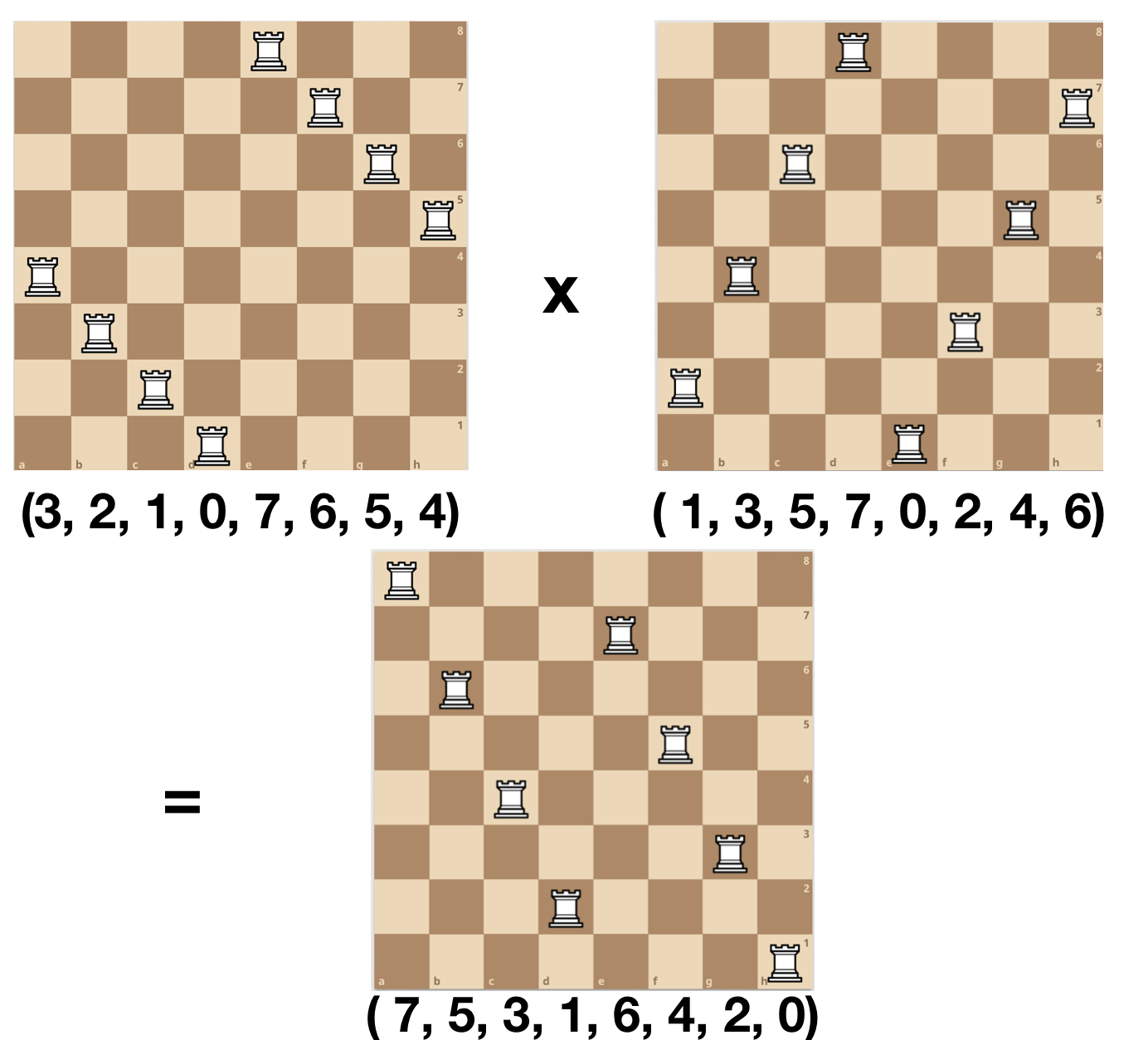
To show how to “multiply” these two solutions to get a new one, you just compose their two permutations as functions. So for example, the first permutation takes 0 to 3, while the second permutations takes 3 to 7, so the composition of the two takes 0 to 7, and so on. We can show their group product graphically like this:

So how many solutions on the n-board are there? From our theorem above we know the answer, which is the same as the number of permutations of $n$ objects, which is to say $n! = 1*2*3*4*….*n$ (n factorial). For the 8×8 board, this works out to 8! = 40320 solutions.

Now how about $B_\omega$, the omega Board? How many solutions? We know from our theorem the friendly Rook positions correspond to the elements of the permutation group $Sym(\mathbb{W})$, where $\mathbb{W}=\{0,1,2,3,…\}$, the set of whole numbers. Now the set of whole numbers is infinite, and has cardinality $\aleph_0$, so is countably infinite. But how many permutations of this set are there?
We will have to do some transfinite arithmetic. To specify a permutation $\phi$ on $\mathbb{W}$ we have to chose values for $\phi(n)$, for every value of n. For n=0 we can pick any of an countably infinite ($\aleph_0$) number of values for $\phi(0)$. Suppose we pick 7. Now how about the next value for n=1? We can’t choose 7, but we still have an infinite number of choices left. And so on. Altogether, we have to make a (countably) infinite number of choices among a countably infinite number of values. This gives us a total count of

$$\aleph_{0} \times \aleph_{0} \times \aleph_{0} \times … =\aleph_{0}^{\aleph_0}$$

solutions. This is an uncountably infinite number of solutions, equal to c, the infinity of the continuum, the number of points on the real line.

Wow. That’s a lot of solutions.

As we will see later, the queen also has a similarly large collection of unguarded solutions, but the Rook is unique in being the only piece of the six whose solutions have a natural group structure.

In the later posts we’ll take a look at the Bishop and queen, and also start to examine fractals and even more infinite boards.