A Chess Puzzle, Part I: The Infinite Chess Board

1/1/2020 Niles Leave a comment

First part of A Mathematical Chess Puzzle:

A while ago I was in the waiting room of the doctor’s office, staring at the ceiling, and looking for something to keep myself amused before the appointment. (The visit was nothing serious, just wanting to update my vaccinations.)

Ceiling at doctor’s office

The ceiling was covered with those white acoustic panels, forming a very large colorless and seemingly infinite chess board. I stared at the tiles, trying to think up some kind of puzzle to keep me amused while waiting. I came up with this:

The Chess Density Problem

Suppose you have an infinite chessboard, and an infinite number of one of the six kinds of chess pieces (King, Queen, Rook, Bishop, Knight, and Pawn). What is the densest packing of “friendly” pieces you can have on that board?

Just asking the question raises more questions:

What do I mean by “infinite” ?
What do I mean by “densest” ?
What do I mean by “friendly” ?
And how would one prove such things?

So far I’ve spend a fair amount of time and scratch paper on this — quite a bit while sitting around with Gigi’s family for Christmas — and have some things to report. The first version of this post was very math-heavy. Now it is a bit lighter. You’re welcome.

Disclaimer

Friends who have suffered through games with me will tell you that I am terrible at playing chess, and spend far too long to come up with a bad move that in standard chess notation would probably be denoted “Nf3 Nc6??”. Not just Chess, but Go, Twixt, Bridge or other strategic games. In defense, I can only say that I am spending all of that time trying to solve the problem, based on the game-theoretic fact that a “best” move exists. The decision tree is so deep, however, that no computer yet exists that can explore it completely more than a few moves ahead.

Good chess players acquire skill through experience and study, making decisions with imperfect knowledge. They stand at the edge of the Grand Canyon of moves and can walk down trails blazed by others. I can only stand at the edge, frozen by the awesome infinitude of the depths. Then I fall in.

Anyway, this isn’t the organic chemistry of Chess, but the simpler math of atoms and fundamental particles, Boards and pieces. Moving on…

Density: A Simple Example

Here is a simple (finite) example of four Queens on a $4 \times 4$ board, where no Queen is attacking any other, either on rank, file, or either diagonal:

Four friendly Queens

So for the $4 \times 4$ board, with its 16 squares, you can only “pack” at most four queens, meaning the “density” (which I denote $\delta$) of Queens on this board is

$$\delta = 4/16 = 1/4$$

Is this the “best” we can do in this case? The answer is yes, for the simple reason that at most one Queen can be on each row (or they would not be friendly), and there are four rows.

What is Already Known

This “packing” puzzle is what’s known as a Mathematical Chess Problem, and falls in the category of “recreational mathematics”. That is, mathematics done for amusement rather than “professional” work on “serious” problems. It should be noted, however, that often these problems lead to questions which are actually “deep” and lead to more important work.

In any case, from the literature, the task of arranging “friendly” chess pieces is called an Independence Problem (or an “Unguard” problem), and a chess position in which all of the pieces are friendly is called “Unguarded”. If an unguarded position is the “best” we can do (ie, there is no unguarded position with more pieces), we will call it maximally unguarded.

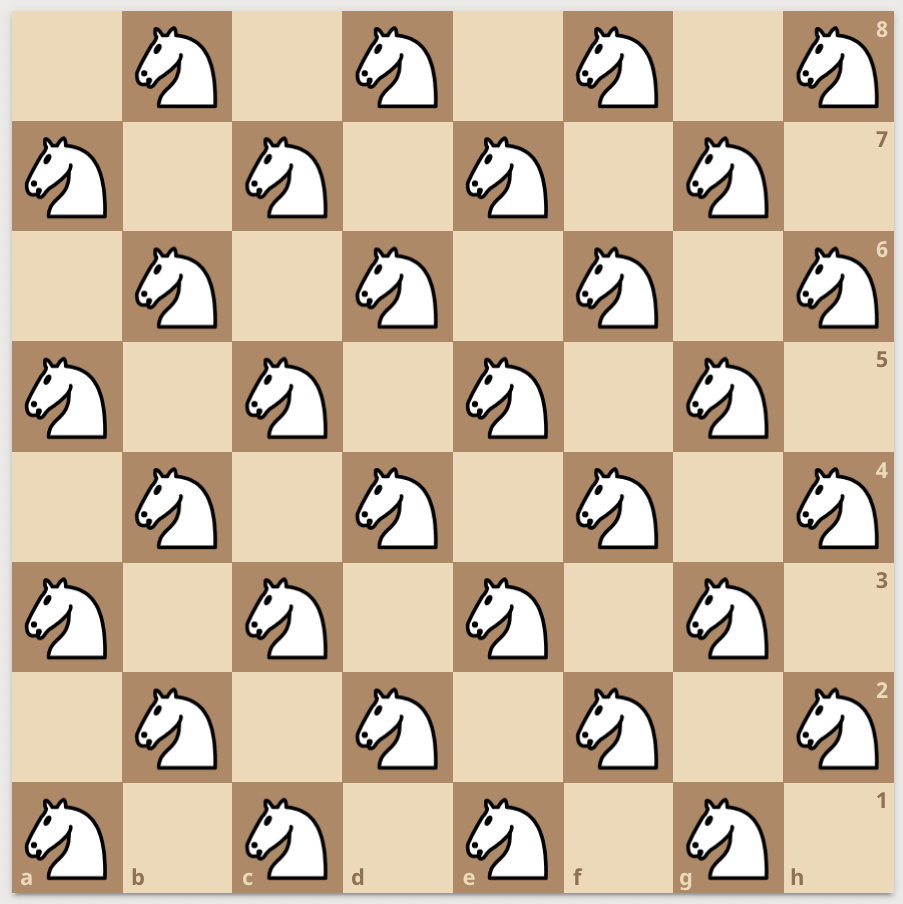
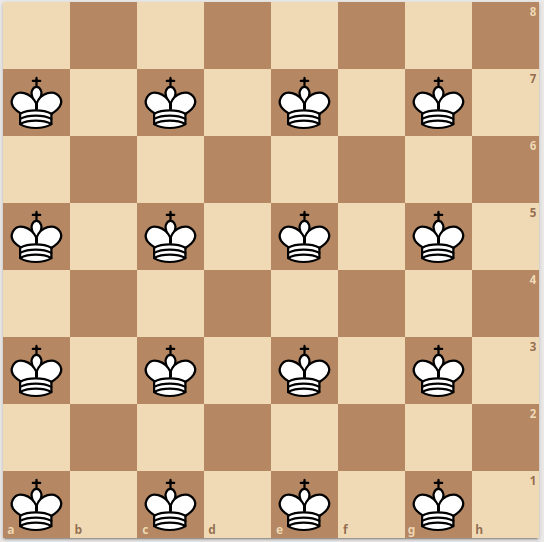
So, for example, on the standard $8 \times 8$ chessboard, here are examples of how to arrange “friendly” Pawns, Knights and Kings:

32 Friendly Pawns

32 Friendly Knights

16 Friendly Kings

We will show (later) that these are “maximally unguarded” positions, and so the density of these pieces on the standard 8-board are 1/2, 1/2, and 1/4, respectively.

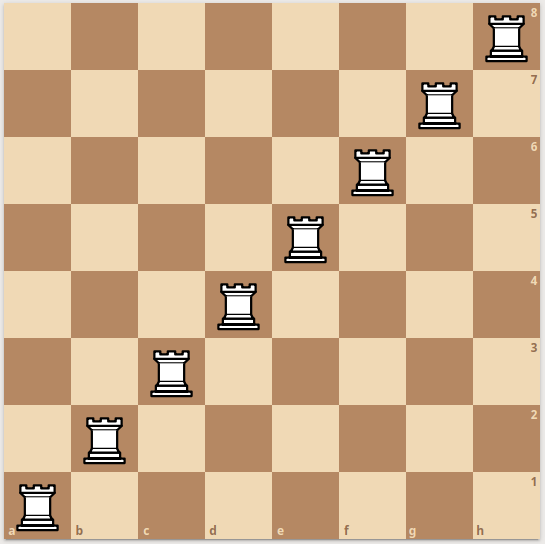
And here is how to arrange the remaining three “friendly” pieces, the Rooks, Bishops and Queens:

8 Friendly Rooks

14 Friendly Bishops

8 Friendly Queens

These last three are maximally unguarded positions, and so the density for these three pieces on the standard board are 1/8, 7/32, and 1/8, respectively.

To see this in the case of the Rooks and the Queens, we can use the same argument as we did above with the Queens on the 4-board, by noting that there are exactly 8 rows and only one Rook or Queen can be on any row.

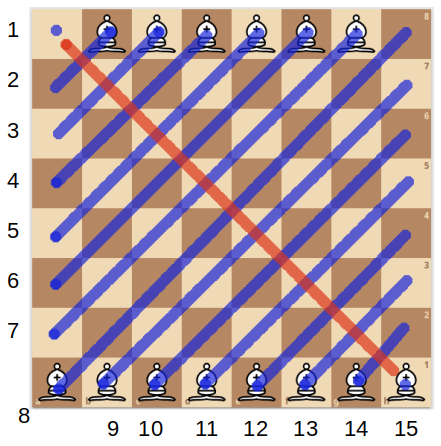
For the 14 Bishops, you can make a similar argument, by noting two things:

There are exactly 15 diagonals in one direction (shown below in blue), and
For each diagonal numbered 1 and 15, there is only one square available for placing a Bishop, and those two squares are “hostile” along the red diagonal, so you can only choose one.

Fifteen Bishop Diagonals

We have separated out the pieces into these two sets of three, because each set have their own unique characteristics, unlike the other set; and the differences in density become more pronounced as the size of the boards becomes larger and becomes infinite. Not only that, but the kind of “density” has to be defined differently, and even the size of the “infinite” board becomes important; as we’ll see, some chess boards are more infinite than others.

Chess Boards: Finite and Infinite

All of the “chess boards” we will be working with will be two-dimensional, and each “square” on which a chess piece can be placed can be indicated by a pair of numbers $(x,y)$, where $x$ and $y$ are coordinates in some set $A$, which we will call the Address space. A chess board that uses coordinates in Address space $A$ will be denoted $B_A$. Mathematically, the board $B_A$ can be identified with the Cartesian product $A \times A$.

For example, the squares of our standard $8 \times 8$ chess board can be specified using $A = \{0,1,2,3,4,5,6,7\}$. The set of integers from 0 to 7 is sometimes denoted $\mathbb{Z}_8$, and so the standard chess board is $B_{\mathbb{Z}_8}$. To make life simple(r), we will also call this board $B_8$, or simply the “8-Board”, and similarly an $n \times n$ board (where n is an integer) will be called the “n-Board”, or $B_n$.

Here for example is the 5-board $B_5 = B_{\mathbb{Z}_5}$:

The 5-Board

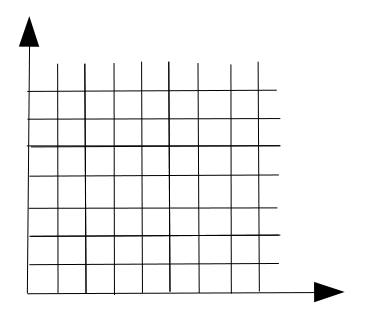
Okay, so far so good (you still with me, here?). Now the point of all this mathematical gobbledegook (a scientific term), is that I wanted to look at the “Unguarded” chess problem on an infinite chess board, meaning that I want to use for a “coordinate space” $A$ an infinite set. The first one that comes to mind is the set of whole numbers, ie

$$\mathbb{W} = \{0,1,2,. . .\}$$

And so we can define our first infinite chess board as $B_{\mathbb{W}}$, consisting of all $(x,y)$ where $x$ and $y$ are non-negative integers.

Intuitively, the board can be visualized like this:

The ω-Board

This picture looks a lot like the ceiling at my doctor’s office, which is what started this whole thing.

Now the “size” (cardinality) of the whole numbers is “infinite”, but the specific mathematical name for this “infinite” value is $\aleph_0$ (pronounced aleph-null). Unlike the conventional symbol for infinity ($\infty$), $\aleph_0$ has a more precise meaning, and it refers only to “countably” infinite sets, ie, those which you can count with the integers 1,2,3, etc. A related infinite “ordinal” number is called $\omega$ (small omega), and with some “abuse of notation” we will refer to $B_{\mathbb{W}}$ as $B_{\mathbb{\omega}}$, or simply the $\omega\text{-Board}$.

Chess Boards: Infinity and Beyond

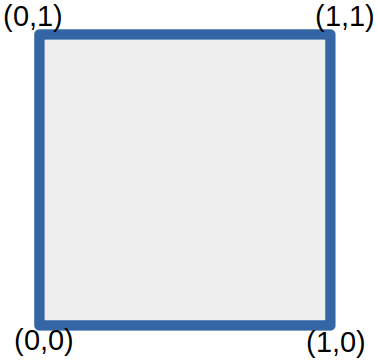
There are many other ways to define infinite boards, but for now the only other board we will look at uses as its coordinate space the closed unit interval on the real line, that is,

$$I = \{ x \in \mathbb{R}: 0 \le x \le 1 \}$$

The board $B_I$ can be visualized as the unit square, including every single point on the boundary and in the interior as a distinct “square” on which you could place a chess piece:

The c-Board

The size of the set of real numbers in $I$ is a transfinite number which is infinitely larger than $\aleph_0$, and is called simply $c$, the infinity of the continuum. If we embrace “The Continuum Hypothesis“, this number c can be identified as $\aleph_1$, the next largest infinity. We shall therefore also call $B_I$ the c-Board, or $B_c$. The number of “squares” on $B_c$, unlike the $\omega\text{-Board}$, is uncountably infinite.

Sneak Preview

The “density” results for each infinite board and piece will be shown (in later posts) to be as follows.
The pieces are in order of their decreasing (2d or fractal) density, and thus their increasing “power”:

$$\omega\text{-Board}$$

Piece	Board	2d-Density	Fractal Dimension	1d-Measure (**)
Pawn	$B_\omega$	1/2	2	*
Knight	$B_\omega$	1/2	2	*
King	$B_\omega$	1/4	2	*
Rook	$B_\omega$	0	*	*
Bishop	$B_\omega$	0	*	*
Queen	$B_\omega$	0	*	*

$$c\text{-Board}$$

Piece	Board	2d-Density	Fractal Dimension	1d-Measure (**)
Pawn	$B_c$	*	*	*
Knight	$B_c$	*	*	*
King	$B_c$	*	*	*
Bishop	$B_c$	$0$	$1$	$2\sqrt 2$
Rook	$B_c$	$0$	$1$	$2$
Queen	$B_c$	$0$	?	?

(*) Not Defined for this piece on this board.

(?) Unknown whether a Hausdorff-measurable solution exists.

(**) 1d-Measure = (Hausdorff Content)

As you can see from the two tables, there is something very different between the two groups of pieces, and how they “pack” on those infinite boards. In following posts, I will try to explain what the differences are, what a Fractal Dimension is, and what other mathematical issues and questions arise in the process.